√ダウンロード 三角定規 角度 なぜ 258633-三角定規 角度 なぜ

小４の壁 三角定規の組み合わせ角度 算数の始めの取り組み Extend

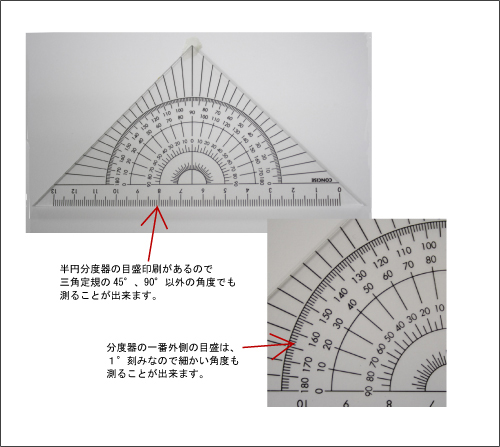
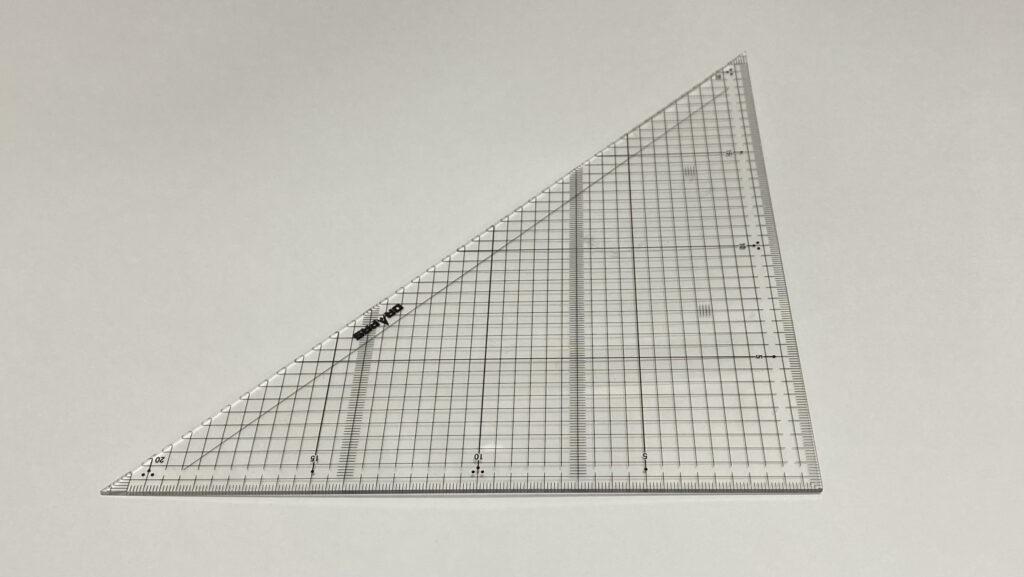
使用法 製図用に用いられる三角定規は、角が45°・45°・90°（直角二等辺三角形）の三角定規と、角が30°・60°・90°（正三角形の半分、半正三角形）の三角定規の2枚一組となっている 。 一組の三角定規において、直角二等辺三角形の斜辺（45°45°の辺）と、半正三角形の長いほうの隣辺（90°30追加雑学三角定規の穴はなぜ丸が多い？ ここまで三角定規の穴は凄いということを解説してきたが、1つ疑問が残る。「穴だったら形はなんでもいいのではないか？」ということだ。 孫ちゃん うんうん。ハート型とか星型とか、そんな形の穴があいてたら超かわいい！ 「摩擦を減らす

三角定規 角度 なぜ

三角定規 角度 なぜ-三角定規は､二等辺直角三角形と 直角三角形の2種類はいっています｡ 小学4年生から三角定規を使用しますが 目的は垂直･平行な直線を作図する｡ また､2直線の位置関係が垂直･平行で あるかを調べる時にも使います｡ では､なぜ2個1組みなのか？三角定規は,上記（図1）の2種類の直角三角形である何故,三角定規はこのような形にな ったのであろうなぜ丸い穴が空いているのかそのわけを考えてみたい (1)正三角形,正方形は図形として最も美しい直角は作図で多用されるために,正三角形を 頂点を通る軸で二等分し,正方形を一本の対角線

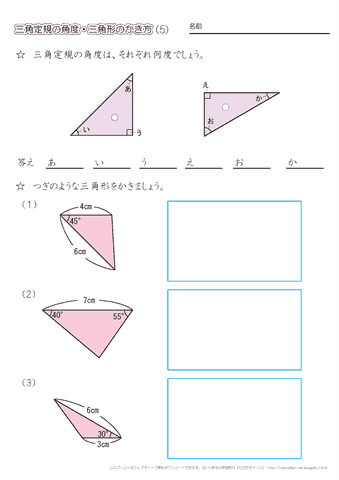
小学４年生の算数 三角定規の角度 分度器を使った三角形のかき方 ちびむすドリル 小学生

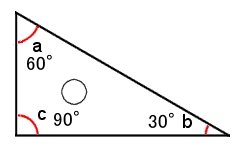
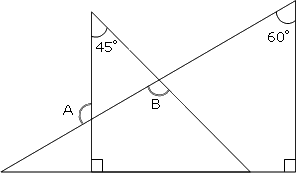
なぜ三角形の和は\(180°\)になるのか？ 下のように合同の三角形を\(3\)つ用意して、すべての内角を足すように並べると一直線になるのが分かります。 一直線の角は\(180°\)なので、内角の和 \(abc=180°\) になります。 これはどんな三角形でも同様です。 この説明だけでは「どんな三角形で数学 三角定規はなぜ2個1組 道具は、分度器も使っていくようになり 三角定規も必要になります。 まだまだ良いことが たくさんあったので、 まとめました。 三角定規を組み合わせた角度の問題 三角定規を組み合わせた角度の問題とは こんな感じです。目次 三角定規の真ん中に穴が開いている2つの理由！ 理由①プラスチック定規の伸縮や変形を防ぐため 理由②摩擦を減らし、すべりを良くするため おまけ：三角定規の穴は丸型が多いのはなぜ？ （星形やハート型じゃダメなの？ ） この記事のまとめ

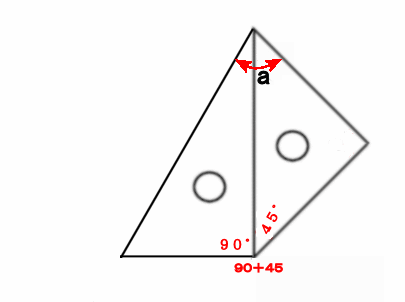
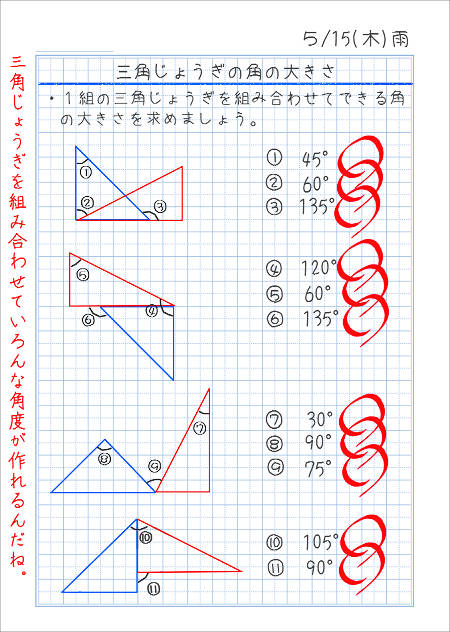
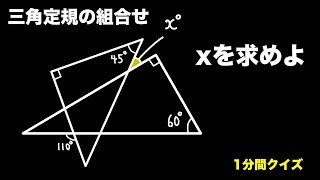
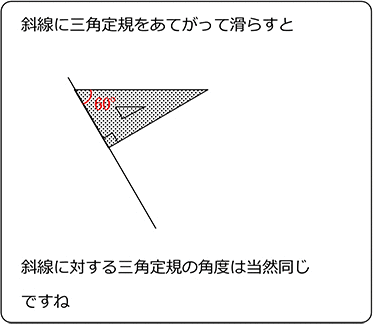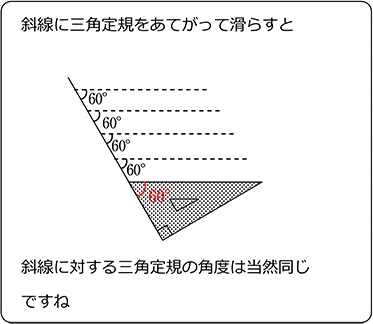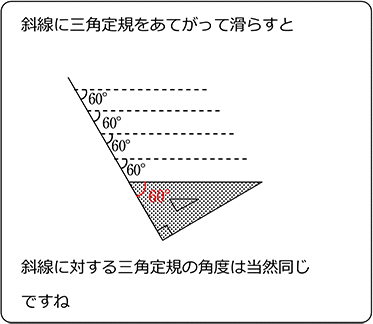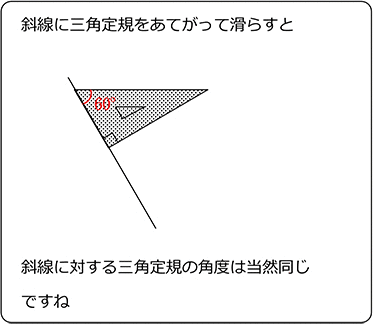
～三角定規でいろいろな角度を作ってみよう。 森竹高裕 角の授業が終わったのでまとめの学習をした。三角定規を使っていろいろな角の大きさを作る活動を通して、角の概念を深めたり三角定規で作った角の大きさには決まりがあることを見つけた。まずこれまでの学習を振り返った。 発問1

三角定規 角度 なぜのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	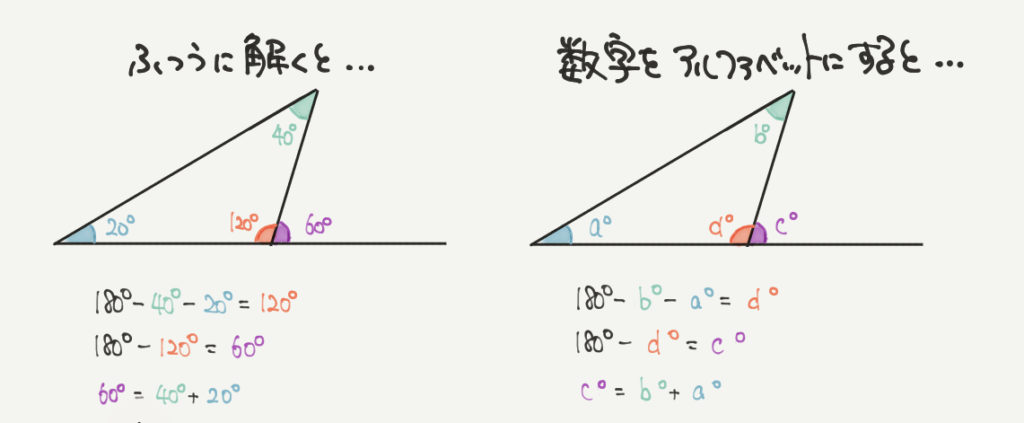三角定規２枚で作ることのできる角度 算数を究める	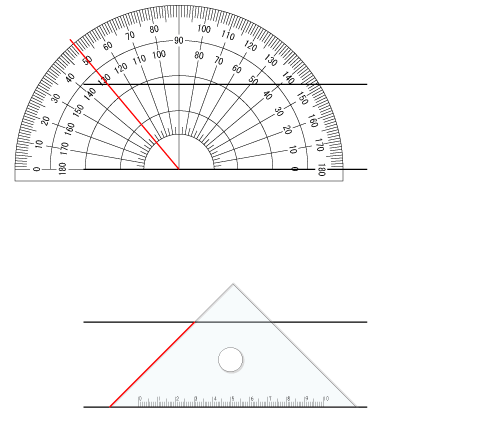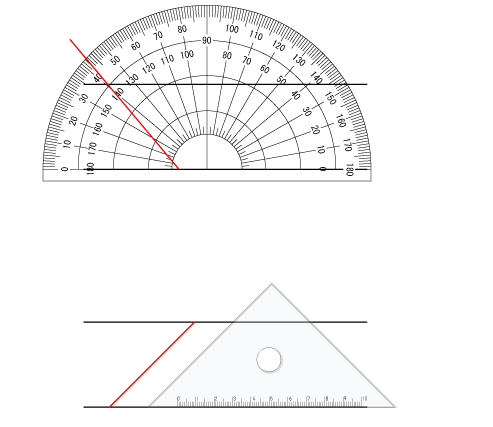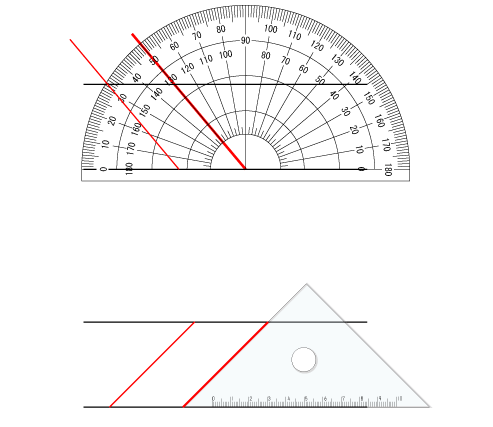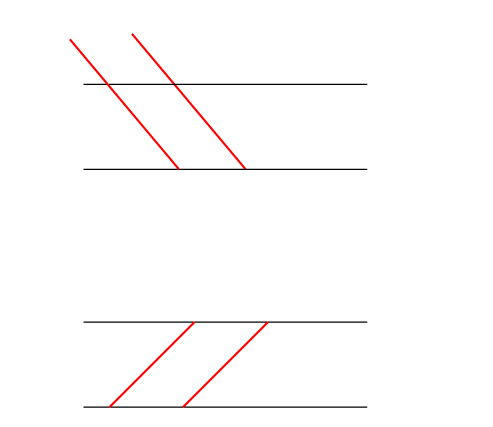三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	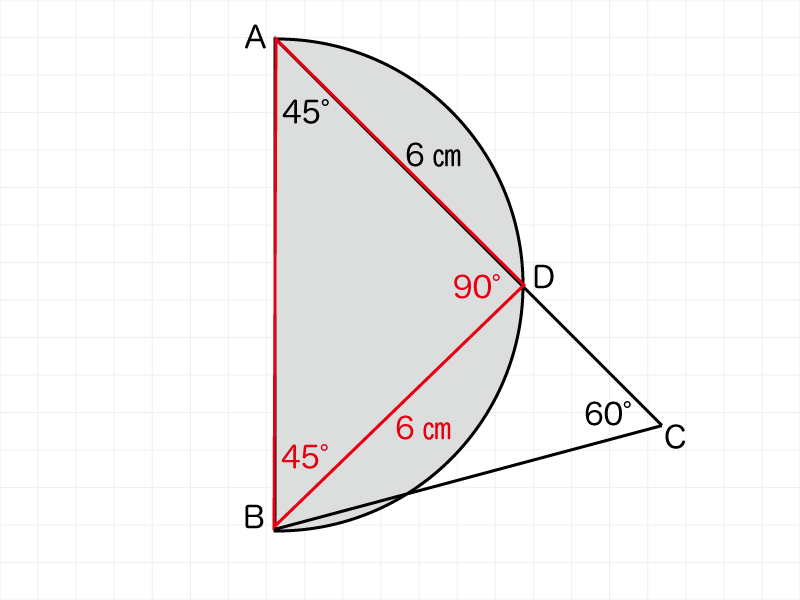三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	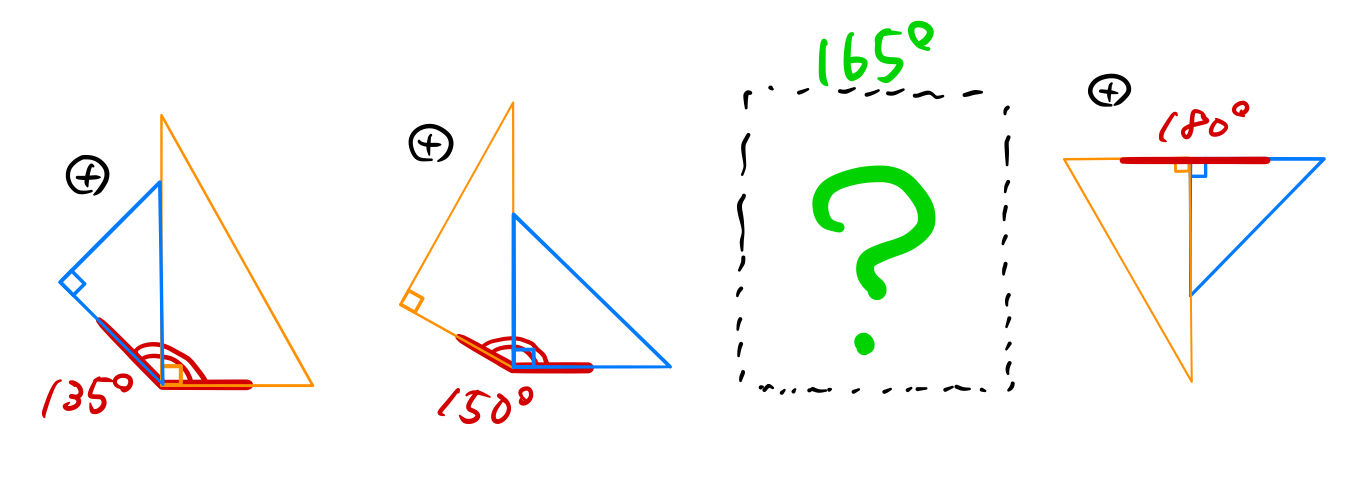三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	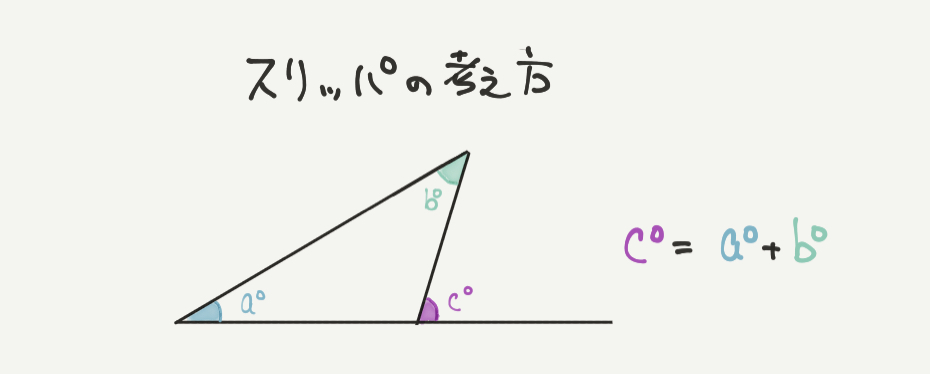三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	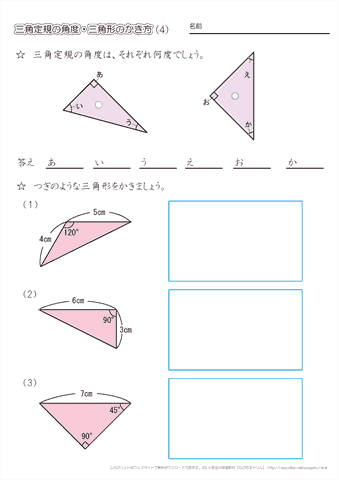三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	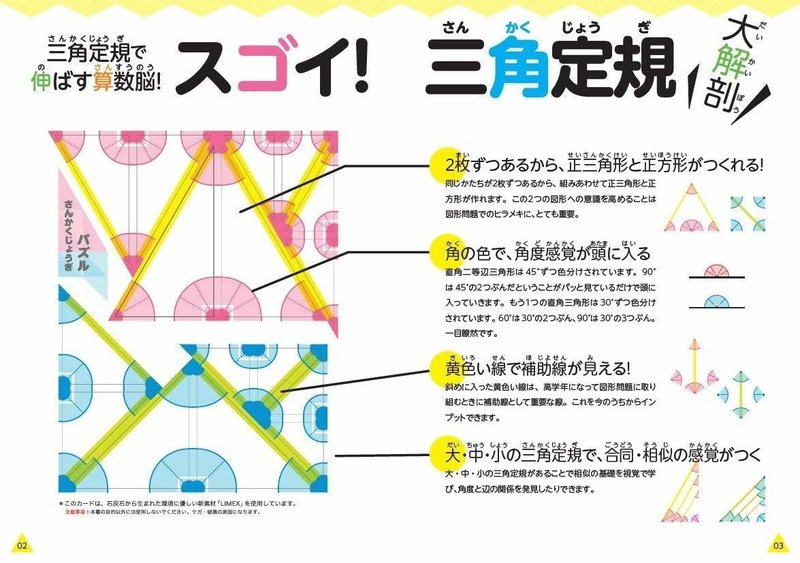三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	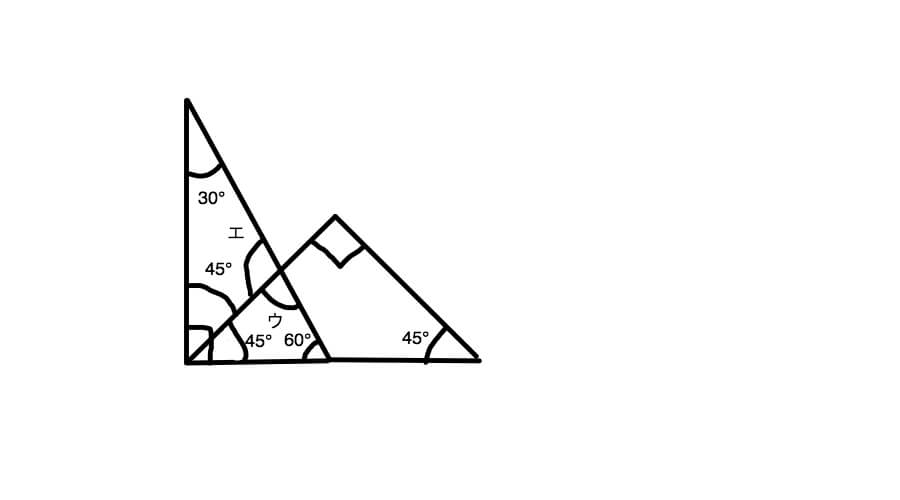三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める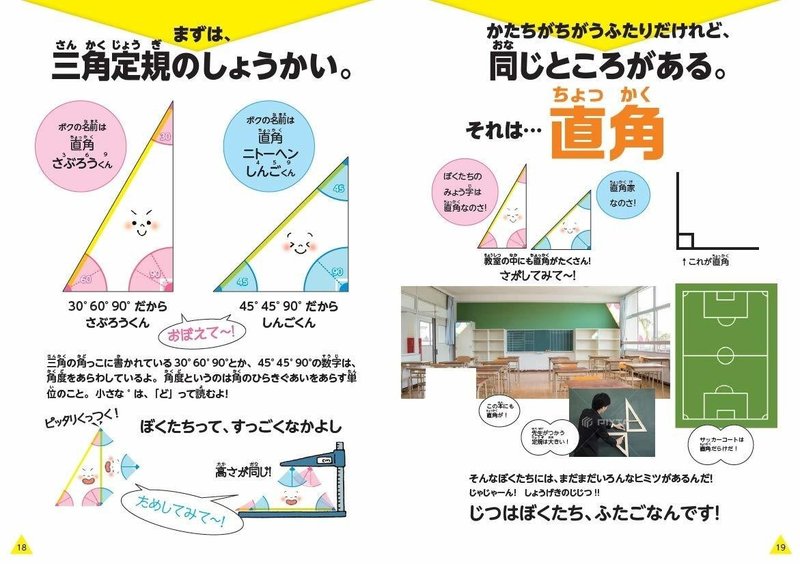
三角定規２枚で作ることのできる角度 算数を究める	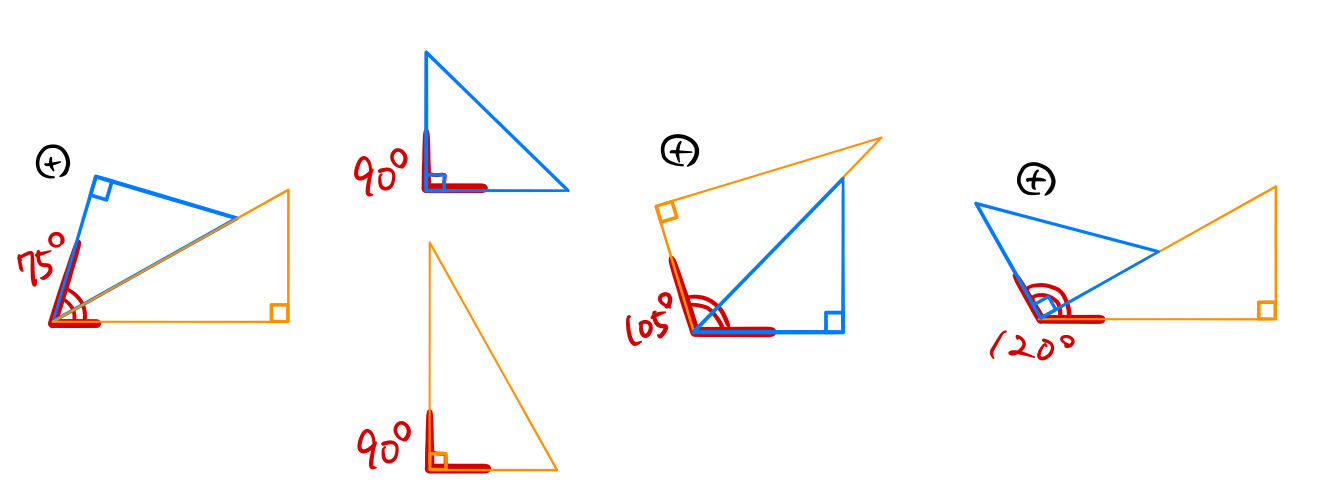三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める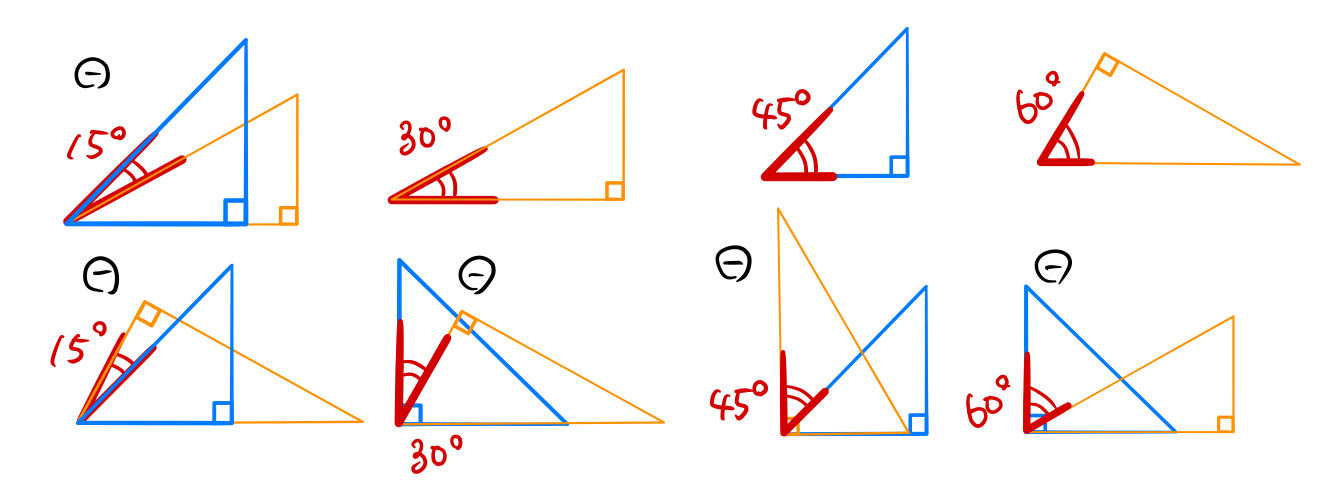
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める
三角定規２枚で作ることのできる角度 算数を究める	三角定規２枚で作ることのできる角度 算数を究める

Incoming Term: 三角定規 角度 なぜ,